Se simboliza por:
Y viene a ser la suma de los productos de la derivada parcial de una o más funciones por sus respectivos diferenciales, es decir:
Si: W=f(x, y, z) ; x= f(t) , y= f(t) , z= f(t)
Ejemplo:
Existen varias formas de resolver este ejercicio pero teniendo en cuenta las formulas estudiadas solo daremos a conocer dos formas de solución:
Solución 1:
Primero derivamos “V” en cada una de sus variables:
Luego derivamos las mini funciones (x, y, z) con respecto a la variable “t”:
Luego aplicamos la fórmula:
Y reemplazamos las variables x, y , z por sus equivalencias en función de “t”
Solución 2
Reemplazamos en la formula principal (V) los valores en función de “t”
La nueva función la derivamos con respecto a “t”
La solución 2 no respeta la fórmula y aparentemente resulta más fácil de hacer, sin embargo, no siempre es efectiva existen casos en los cuales la solución 2 no es la apropiada.


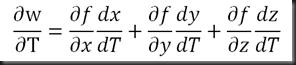

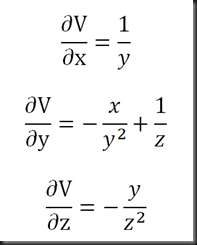

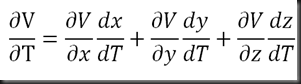

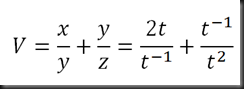
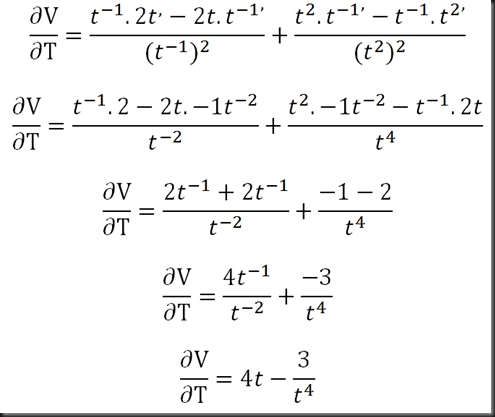

No hay comentarios:
Publicar un comentario