Una Ventana de Negocios by Lizer® Corp®
Es el punto temporal donde se suman o se comparan los capitales, es decir, en el caso de que tengamos dos capitales en dos fechas distintas para compararlos se puede hacer uso de la actualización y la capitalización.
Ejemplo
Si tenemos dos capitales uno dentro de 5 años a una tasa del 15% anual por un monto de 2000 y otro dentro de 7 años por un monto de 4000 a una tasa del 20%, a un interés simple, ¿Cuál de los dos capitales es mayor?
Operación financiera.- actividad que motiva un cambio en la cuantía de una capital
Stock.- no está en movimiento una cantidad de dinero (en un momento dado en el tiempo)
Stock inicial de efectivo (P).- valor presente, valor actual o valor liquido
Stock final de efectivo (S).- monto, suma de valor inicial más los intereses, valor futuro.
Tasa de interés (i).- es la diferencia entre el monto o stock final y el importe original que lo produjo; es la acumulación de todo solo intereses.
Periodo (n).- Es el número de periodos de interés en el tiempo
Flujo de periodos, flujo constante (A).- es una serie consecutiva igual de dinero al final de cada periodo.
Capitalización.- es la acumulación del dinero a través del tiempo y va de presente a futuro
Actualización.- es la desacumulación del dinero y va del futuro al presente.
B= cantidad base
T= tasa o tanto por ciento
P= porcentaje
Ejemplo:
25% de $ 80 = $ 20
Dónde:
25% es la tasa
$ 80 es la base
$ 20 es el porcentaje
Da clic para seguir el vínculo:
CASO 1
Si se comienza ahora a hacer 5 depósitos de $ 100 por año en una cuenta que paga el 18% anual ¿Cuánto dinero se abra acumulado inmediatamente después de que se halla hecho el último pago?
CASO 2
Si usted solicita un préstamo de 2000 dólares y debe pagar la deuda más los intereses a una tasa del 12% por año en 5 años ¿Cuál es la cantidad que debe pagar?
CASO 3
Suponga que desea hacer un deposito en una cuenta de ahorros de tal manera que s epoda retira una cantidad igual anual de 1000 dólares por año durante los primeros 5 años comenzando un año después de su depósito y una cantidad anual diferente de 400 dólares por año, los siguientes 3 años, como será el diagrama de flujo de caja se i=14,5%
CASO 4
Si usted recibe un préstamo por 5000 dólares debe pagar el préstamo más los intereses a una tasa del 4% en 5 meses
CASO 5
Si usted deposita 10000 dólares en una cuenta de ahorro y le pagan el 7% mensual, ¿Cuánto puede usted retirar a los 10 meses siguientes?
CASO 6
Si usted recibe hoy un préstamo de 8000 dólares al 5% anual por 5 años y debe devolver el préstamo al final de cada año, ¿Cuánto debió pagar?
Ejemplo:
Si se desea pagar las obligaciones que a continuación se indican mediante dos importes uno al sexto y otro al noveno mes ambos iguales tomando como fecha focal el fin de mes 12, siendo la tasa de interés del 9% mensual, calcular el valor de cada pago.
| Dólares | Tiempo |
| 10000 | 5 meses |
| 12000 | 7 meses |
| 15000 | 8 meses |
| 13000 | 12 meses |
Desarrollo:
x (1 + 0,09)6 + x (1 + 0,09)3 = 10000 (1 + 0,09)7 + 12000 (1+0,09)3 + 15000 (1 +0,09)4 + 13000
x = $ 23860,88
16% en un año es un 16% de interés simple
16% en un año es un 16% más un plus de interés compuesto
Porque el 16% es una tasa nominal y la tasa efectiva es el verdadero cobro de intereses.
Así tenemos que:
Las tasas de interés efectivas tienen siglas específicas:
| Intereses | Siglas |
| Anual | TEA |
| Semestral | TES |
| Cuatrimestral | TEC |
| Trimestral | TET |
| Bimestral | TEB |
| Mensual | TEM |
| Quincenal | TEQ |
| Diaria | TED |
Ejemplo:
Un banco paga por los depósito que recibe una tasa nominal mensual del 3% con capitalización trimestral , que monto se habrá acumulado con un capital inicial de 3000 dólares en 6 meses
Datos
P= $ 3000
i= 0,03 TEM
n= 6 meses
Capitalización trimestral
Desarrollo:
Primero convertimos a la tasa en trimestral:
0,03 x 3 = 0,09 TET
Luego convertimos a los meses en trimestres:
6/3 = 2 trimestres
Luego hallamos el monto:
S = 3000 (1+ 0,09)2
S = 3000 (1,048808848)
S = $ 1048,81
La diferencia de estos beneficios básicamente es:
Costo= tasa de interés incremente
Venta= tasa de interés disminuye
Pero ambos son equivalentes en su valor monetario.
Da clic para seguir el vínculo:
Es la diferencia ente el precio de venta con beneficio sobre la venta y el precio de venta con beneficio sobre la compra.
Se entiende como la rebaja que se le puede dar a un producto, Ejemplo:
Se compra un producto por valor de $ 18,90 y se quiere obtener un beneficio del 24%, calcular el precio de venta en forma detallada y en forma directa.
a) Con beneficio sobre el precio de costo
b) Con beneficio sobre el precio de venta
c) Hallar la diferencia de cálculos.
Desarrollo de “a”
Precio de compra $ 18,90
+24% beneficio sobre el precio de compra $ 4,53
Precio de venta $ 23,43
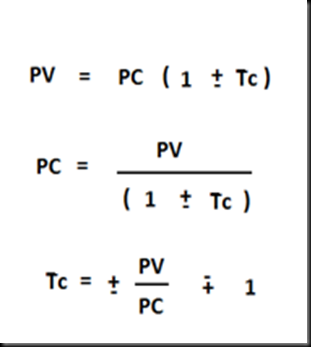
Por formula:
PV= 18,90 (1 + 0,24)
PV = $ 23,43
Desarrollo de “b”
Precio de venta base 100%
-24% de beneficio sobre el precio de venta 24%
Precio de costo base 76%
Lo que se compra en $ 76 se vende en $ 100
Lo que se compra en $ 18,9 se vende en $ 24,86
Desarrollo de “c”
Precio de venta con beneficio sobre la venta $ 24,86
-precio de venta con beneficio sobre la compra $ 23,43
Diferencia de cálculo $ 1,43
Son representaciones graficas del flujo de ingresos y egresos que ocurren en el tiempo.
Da clic para seguir el vínculo:
Se utiliza cuando se ha hecho un descuento sobre un producto, es decir, es igual al precio de venta bruto sobre el precio de venta neto, la fórmula del coeficiente de descuento es:
Ejemplo:
¿Qué precio debe fijarse a un producto para que después de conceder el 20% de descuento se obtenga un precio de venta neto de $ 36,92?
Datos:
D= 20%
PVN= $ 36,92
Calculo del coeficiente de descuento
Coeficiente = 100/(100-20)
Coeficiente = $ 1,25
Calculo del precio de venta bruto
PVB = 1,25 x 36,92
PVB = $ 46,15
Comprobación:
PC = PV (1-Tv)
PC = 46,15 ( 1- 0,2)
PC = $ 36,92
se hace uso de las siguientes fórmulas:
ejemplo:
hallar la tasas nominales que convertibles semestral, trimestral, mensual y diariamente equivalen a una tasa efectiva de 24%
datos:
J= ?
i = TE = 24%
m = 2, 4, 12, 360
desarrollo:
a) m=2
J = 2 ((1+0,24)1/2-1)
J=22,71%
b) m=4
J = 4 ((1+0,24)1/4-1)
J= 22,10%
c) m=12
J = 12 ((1+0,24)1/12-1)
J= 21,71%
d) m=360
J = 360 ((1+0,24)1/360-1)
J= 21,52%
Recuerda, a mayor número de capitalizaciones menor es la tasa nominal.
Se usan las siguientes formulas:
Ejemplo:
Hallar las tasas efectivas que se obtendrían de una tasa nominal de 15% si las conversiones hicieran:
a) Trimestral
b) Semestral
c) Mensual
d) Diariamente
Desarrollo:
a) m=4
i= (1+0,15/4)4-1
i=15,87%
b) m= 2
i= (1+0,15/2)2-1
i=15,56%
c) m=12
i= (1+0,15/12)12-1
i=16,07%
d) m= 360
i= (1+0,15/360)360-1
i=16,18%
Para deducir el interés compuesto en un periodo de capitalización podemos hacer uso del siguiente cuadro:
| Horizonte de tiempo | Stock inicial | Interés | Stock final |
| 0 | | | P |
| 1 | P | P x i | P + Pi = P (1+i) |
| 2 | P(1+i) | P (1+i) x i | P (1+i) + P (1+i) x i = P (1+i) (1+i)= P (1+i)2 |
| 3 | P(1+i)2 | P (1+i)2 x i | P (1+i)2 + P (1+i)2 x i= P (1+i)3 |
| 4 | P(1+i)3 | P (1+i)3 x i | P (1+i)3 + P (1+i)3 x i= P (1+i)4 |
| … | … | … | … |
| n | P(1+i)n-1 | P (1+i)n-1 x i | P (1+i)n-1 + P (1+i)n-1 x i= P (1+i)n |
(Análisis de sensibilidad de variación de la fórmula de interés compuesto)
Tenemos las siguientes formulas:
Ejm:
Hallar el capital que hay que imponer al 8% durante 220 días para obtener un monto de 10000 dólares.
i= 8% anual
n= 220 días : 220 / 365
S = $ 10000
Una máquina cuyo precio de contado es de 6000 dólares fue adquirida con una cuota inicial de 2000 dólares y el saldo financiado con una letra de 45 días por un importe de 4500 dólares, ¿Cuál es la tasa mensual de interés simple cargada?
Datos:
P = 4000
S = 4500
n = 45 días
i = ?
Desarrollo:
Para hallarlo a partir de descuento sucesivos se usa esta fórmula:
Dónde:
DC= descuento comercial
PV=precio de venta.
d= descuentos sucesivos.
Cuando se hace uso del signo positivo se llama aumento comercial y cuando se hace uso del signo negativo es un descuento comercial.
Ejemplo:
El precio de venta de un artículo es de $ 16,4; si se vende con descuento de 12 ½% y 10%, hallar el descuento comercial
DC=16,4(1-(1-0,125) (1-0,10))
DC= $ 3,48
Para hallarlo a partir de descuento sucesivos se usa esta fórmula:
DU= descuento único
d= descuentos sucesivos.
Ejemplo:
El precio de venta de un artículo es de 16,4, si se vende con descuento de 12 ½% y 10%, hallar tanto por ciento equivalente
DU= (1-(1-0,125) (1-0,1))
DU= 21,25%
Se obtiene colocando en un diagrama de tiempo- valor líneas rectas verticales cada periodo y estas dirigidas hacia abajo cuando son egresos, y dirigidos hacia arriba cuando son ingresos.
Da clic para seguir el vínculo:
Consiste en una línea (recta) horizontal dividida en espacios iguales denominados periodos , si en línea de tiempos (horizonte temporal) se colocan los valores que intervienen , se tiene un diagrama de tiempo valor.
En un diagrama el tiempo puede medirse en dos momentos diferentes:
Sentido proyectivo.- de izquierda a derecha
Sentido retrospectivo.- de derecha a izquierda
Solo sirven para dar información
El diagrama representa el planteamiento del problema y muestra que el lo dado y lo que debe encontrarse.
Se utiliza sobre todo cuando existen varios productos de diferente valor cada uno, también se puede decir que el coeficiente de beneficio es igual al precio de venta neto sobre el costo, para hallarlo se usa la fórmula del coeficiente de beneficio:
Ejemplo:
Un comerciante compro un lote de artículos por el precio de 24 soles, 36 soles y 18 soles, y quiere ganar el 35% de las ventas netas, ¿Cuál es el precio de venta marcado?
Datos:
B= 35%
PC= $ 24, $ 36 y $ 18
Calculo del coeficiente de beneficio
Coeficiente de beneficio = 100/(100-B)
Coeficiente de beneficio = 100/(100-35)
Coeficiente de beneficio = 1,538461538
Calculo de los precios de venta netos
PVN = CB x Costo
Donde
PVN: precio de venta neto
CB: coeficiente de beneficio
PVN= 1.538461538 x 24
PVN= $ 36,92
PVN2= $ 55,38
PVN3= $ 27,69
El mismo ejercicio explicado de forma detallada:
Precio base: $ 100
-35% de beneficio $ 35
PC base $ 65
Precio de venta neto
65 PC - $ 100
24 PC - $ X1
X1= $ 36,92
Y así se resuelven los otros dos precios.
El mismo ejercicio hallado de forma directa:
Precio de venta neto:
Por formula de beneficio sobre la venta:
Se halla PV1 = 24/(1-0.35)= $ 36,92
Se utiliza cuando se ha hecho compra de varios productos y a la vez se han hecho descuentos, también es conocido como el coeficiente del precio de venta bruto, la fórmula del coeficiente dado el beneficio y descuento es:
Ejemplo:
Un comerciante compro un lote de artículos a 24 soles, 36 soles y 18 soles, quiere ganar el 35% de las ventas netas después de conceder al cliente el 20% de descuento, hallar el coeficiente dado el beneficio y el descuento.
Datos:
B=35%
D=20%
Calculo del coeficiente de venta bruto
CPVB= (100 x 100) / ((100-35)(100-20))
CPVB = 1,923076923
Calculo del precio de venta bruto
PVB= CPVB x costo
PVB1= 1,923076923 x 24
PVB1= $ 46,15
PVB2= $ 69,23
PVB3= $ 34,61
Cálculo del porcentaje
Para hallar el porcentaje se usa la siguiente formula:
Dónde:
B= cantidad base
T= tasa o tanto por ciento
P= porcentaje
Cálculo de la base
Se usa la siguiente formula:
Cálculo de la tasa o tanto por ciento
Se usa la siguiente formula:
Nota, en las operaciones matemáticas de tanto por ciento el término “de” significa multiplicación.
Ejemplo: Hallar el 7.94% de 200000
Se hace uso de esta fórmula cuando se ha hecho uso de un beneficio sobre el precio de venta a un producto y se desea hallar el precio de compra o el precio de venta.
Las fórmulas para el desarrollo de estos problemas son:
Ejemplo:
Un artículo se vendió en 3000 dólares perdiendo el 30% del precio de venta, ¿a qué precio se compró?
Precio de venta base 100%
+30% de pérdida sobre el precio de venta 30%
Precio de compra 130%
PC = 3000 (1 + 0.3)
PC= 3000 (1.3)
PC = $ 3900
Comprobación a través de la regla de tres simple:
Lo que se compro en $ 130 se vende en $ 100
Lo que se compro en $ 3900 se vende en $ 3000
Es la ganancia obtenida teniendo como base al precio de venta, su fórmula comercial es:
PV= precio de venta
PC=precio de compra
Tc= tasa de beneficio o perdida sobre la venta
Recuerda, el signo superior de la formula (-) es si se espera un beneficio y el inferior si es una perdida (+) .
Ejemplo:
Se compra una mercadería de valor de $ 230 y se requiere obtener un beneficio del 30% sobre el precio de venta, calcular el precio de venta al público.
Precio de venta base 100%
-30% de beneficio sobre el precio de venta 30%
Precio de costo base 70%
Aplicando formula:
PV = 230/(1-0,30)
PV= $ 328,57
Comprobación a través de la regla de tres simple
Lo que el comerciante compra por $ 70 se vende en $ 100
Lo que el comerciante compra por $ 230 se vende en $ 328,57
Es la ganancia que se obtiene sobre el precio de compra, su fórmula comercial es:
PV= precio de venta
PC= precio de compra
Tc= tasa de beneficio perdida sobre la compra
Recuerda, el signo superior de la formula (+) es si se espera un beneficio y el inferior si es una perdida (-) .
Ejemplo:
Se compra una mercadería por valor de $ 230 y se quiere obtener beneficio del 30% sobre el precio de compra, calcular el precio de venta.
Precio de compra $ 230,00
+ 30% beneficio sobre el precio de compra $ 69,00
Precio de venta $ 299,00
Haciendo uso de la formula:
PV = 230 (1 + 0.30)
PV= 230 (1,30)
PV = $ 299,00
La fórmula para realizar el cálculo de manera más sencilla es:
Ejemplo:
Cierta mercadería se vende en 110 soles ganando el 10% del precio de venta, se desea saber ¿qué tanto por ciento se gana sobre el precio de compra?
La fórmula para realizar el cálculo de manera más sencilla es:
Ejemplo:
Si el precio de los medicamentos se permite una utilidad del 30% sobre el precio de compra, ¿cuál es la utilidad sobre el precio de venta?
Se hace uso de esta fórmula cuando se ha hecho uso de un beneficio sobre el precio de compra a un producto y se desea hallar el precio de compra o el precio de venta.
Las fórmulas para el desarrollo de estos problemas son:
Donde:
PV= precio de venta
PC=precio de compra
Tc= tasa en decimales
Recuerda, el signo superior de la formula si se espera un beneficio y el inferior si una perdida.
Ejemplo:
Se compra un producto por 600 dólares con una ganancia del 25% sobre el precio de compra, calcular el precio de venta y la ganancia.
Precio de compra $ 600
+25% de ganancia sobre el precio de compra $ 150
Precio de venta $ 750
Por formula:
PV = 600 (1+0.25)
PV = 600 (1.25)
PV = $ 750
Puntos básicos:
Los precios son regulados por la oferta y la demanda.
La SBS (superintendencia de banca y seguros) se encarga de supervisar ahorros.
El BCR (Banco central de reserva) supervisa la moneda
Excedente.- cuando los gastos se cubren y queda algo
Valores.- acciones, cedulas hipotecarias, etc.
Superávit.-. ingresos superiores a los egresos
Déficit.- egresos superiores a los ingresos
Concepto
La demanda es la cantidad de bienes y servicios que un consumidor o cliente está dispuesto a comprar a un precio y en un momento determinado.
La demanda está determinada en función a los factores antes mencionados siendo el más importante “Px” precio del artículo
Dx = f (Pe, Po, Pr, Px, X, Y)
Si Dx= f (Px)
La pendiente de la demanda es menor que 0, es decir es de pendiente negativa.
PARA NÚMEROS DISCRETOS
Así se le llama a la relación inversa de precio y cantidad
Función implícita:
4x + 5y = 9
Ejemplo:
Función explicita con respecto a x
X = f(y)
Función explícita con respecto a y
Y = f (x)
Para graficar un plan de demanda se debe tener una función de demanda o las puntas que se cruzan en un plano cartesiano, en el eje “x” va la cantidad demandada “y” en el eje y va el precio del producto. Ejemplo:
Tenemos la función
Dx = 12 – 2px
Tabular
Grafica
A LO LARGO DE LA CURVA DE DEMANDA
Se debe al precio desplaza la cantidad demandada de los puntos “A” a “B” de “B” a “C” y de “A” a “C” y viceversa
DESPLAZAMIENTO COMPLETO DE LA CURVA DE DEMANDA
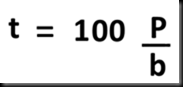
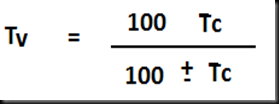
![clip_image002[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEigxgJjr9hpQQbQpcgpJ_cmwDTLrX-YSEBEVhp2JgDO5rel4EugvIxbutMKtRPFIMv6tpTuZJyyxITzhhWCahwmp6quVnj5X0PPmFBVjAJ65UnP6gxOVUBx4Iqke2Az98uouqEkqJpMZFU/s1600-h/clip_image002%25255B5%25255D%25255B2%25255D.jpg "clip_image002[5]")
Ejemplo el ingreso
Si sube el ingreso podemos comprar al mismo precio mayores cantidades
Si baja el ingreso podemos comprar al mismo precio menores cantidades
Se debe a los otros factores que determinan la función de demanda también conocidos como Ceteris Paribus
Ejemplo el ingreso:
Si sube el ingreso podemos comprar al mismo precio mayores cantidades
Si baja el ingreso podemos comprar al mismo precio menores cantidades
![clip_image002[5]_thumb](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhm9aKhRWt3i0TKmmxhKyV1NrLFlvAAMy1pkVoMw_reHF-YQeNI1kn6mqMquVvQx9zTVDBru4dHwOOsH6BjbRx3DQFHNCw1cRJkiw-R6R3-T4yGhH_zv63vQVmPuQt8yYIm9dKYVg85T3Q/s1600-h/clip_image002%25255B5%25255D_thumb%25255B3%25255D.jpg "clip_image002[5]_thumb")